MODUL SPSS

VALIDITAS DAN RELIABILITAS INSTRUMEN

Untuk membantu Anda menguasai hal tersebut di atas dalam modul SPSS ini akan disajikan pembahasan dan latihan dalam butir-butir uraian sebagai berikut :

1. Validitas mencakup: Validitas Internal (Validitas isi, Validitas kriteria, Validitas konstruk) dan Validitas eksternal termasuk cara pengujiannya.
2. Reliabilitas mencakup: Pengertian Reliabilitas dan Cara-Cara Mengukur Reliabilitas termasuk Pengukuran Konsistensi eksternal melalui Metode test-retest dan Metode Bentuk-Bentuk Equivalent serta Pengukuran Konsistensi Internal Prosedur Bagi Dua (split half) dan Pendekatan-Pendekatan Kuder-Richardson ((Kuder-Richardson Approaches).

untuk mengetahui lebih lanjut mengenai isi dari Modul SPSS ini,
silahkan anda mendownload pada link di bawah ini:

DOWNLOAD MODUL SPSS

sumber: file.upi.edu

UJI VALIDITAS KUESIONER PENELITIAN

UJI VALIDITAS KUESIONER PENELITIAN

PENGERTIAN

• Uji Validitas Kuesioner Penelitian: adalah prosedur untuk memastikan apakah kuesioner yang akan dipakai untuk mengukur variabel penelitian valid atau tidak

• Kuesioner yang valid berarti kuesioner yang dipergunakan untuk mengumpulkan data itu valid. Valid berarti kuesioner tersebut dapat digunakan untuk mengukur apa yang hendak diukur.

• Kuesioner ada yang sudah baku, karena telah teruji validitas dan reliabilitasnya, tetapi banyak juga yang belum baku. Jika kita menggunakan kuesioner yang sudah baku, tidak perlu dilakukan uji validitas lagi, sedangkan kuesioner yang belum baku perlu dilakukan uji validitas.

• Kuesioner yang valid harus mempunyai validitas internal dan eksternal. Kuesioner yang valid harus mempunyai validitas internal atau rasional, bila kriteria yang ada dalam kuesioner secara rasional (teoritis) telah mencerminkan apa yang diukur, sedangkan kuesioner yang mempunyai validitas eksternal bila kriteria didalam kuesioner disusun berdasarkan fakta-fakta emperis yang telah ada (eksternal)

• Validitas internal kuesioner harus memenuhi: construct validity (validitas kontruks) dan content validity (validitas isi)

Download Tabel t untuk d.f = 1 – 200

Tabel t yang digunakan untuk pengujian hipotesis (uji t) telah tersedia dan dilampirkan pada buku-buku statistik atau ekonometrik. Namun demikian, tabel tersebut umumnya hanya tersedia secara berurut sampai derajat bebas (d.f./d.b) = 30, kemudian meloncat ke d.f  = 40, d.f. = 60 dan d.f. 120.

Tentunya, jika kita perhitungan kita memiliki derajat bebas 35 misalnya terpaksa harus melakukan interpolasi antara df = 30 dengan df 40.

berikut ini saya lampirkan tabel t yang memuat nilai-nilai t mulai dari df = 1 sampai df = 200 secara berurut.

Silakan di download disini

sumber: (http://junaidichaniago.wordpress.com)

Download Tabel r Lengkap

Buku ajar Statistika kadang-kadang melampirkan tabel r dalam rangka pengujian statistik (misalnya untuk pengujian validitas konstruk). Namun demikian, biasanya  tidak setiap nilai r untuk setiap derajat bebas yang dicantumkan. Oleh karenanya, kita sering kesulitan menentukan nilai r tabel ketika derajat bebas yang kita miliki tidak tercantum dalam tabel tersebut.

Oleh karenanya, berikut ini diberikan tabel r yang relatif lengkap, yang memuat tingkat signifikansi 0.1 , 0.5, 0.02, 0.01, 0.001. Selain itu, tabel ini juga memuat nilai r untuk derajat bebas mulai dari 1 – 200 secara berurut (lengkap).

Bagi yang membutuhkan, silakan download tabel r 

sumber : junaidichaniago.wordpress.com/

Cara Praktis Menghitung Nilai r Tabel Dengan Excel

Beberapa sumber menyebutkan bahwa untuk menghitung nilai r tabel kita harus terlebih dahulu menghitung nilai t tabel . Hal ini karena nilai r tabel dihasilkan dari rumus sebagai berikut:

Dimana: r = nilai r tabel, t = nilai t tabel dan df = derajat bebas

Berdasarkan rumus tersebut, maka  pada Excel dilakukan tahapan sebagai berikut: (lihat gambar dibawah)

Pada kolom A dituliskan derajat bebas (df). Derajat bebas dihitung dengan rumus N-2, dimana N adalah jumlah data. Dalam contoh diatas, kita buat df nya 1 – 5

Kolom B kita gunakan untuk menghitung nilai t tabelnya.  Pada  sel B2 kita tuliskan angka 0,05. Contoh ini adalah untuk mencari nilai t tabel dengan α ( tingkat signifikansi 5%). Kemudian pada sel B3 kita tuliskan rumus berikut:  =TINV(B$2,$A3). Ini adalah rumus untuk mencari nilai t tabel. Selanjutnya, copy rumus tersebut sampai ke sel B7

Kolom C kita gunakan untuk menghitung nilai r tabelnya.  Pada  sel C2 kita tuliskan angka 0,05. Contoh ini adalah untuk mencari nilai r tabel dengan α ( tingkat signifikansi 5%). Kemudian pada sel C3 kita tuliskan rumus berikut:  = =B3/SQRT($A3+B3^2).  Ini adalah rumus untuk mencari nilai r tabel. Selanjutnya, copy rumus tersebut sampai ke sel C7.

Nah, sudah kita dapatkan nilai r tabel.

Tapi, bagaimana kalau kita persingkat tahapannya dengan cara menggabungkan kedua rumus tersebut sehingga lebih praktis. Mari lihat gambar dibawah ini

Sama dengan cara diatas, tapi pada kolom B langsung kita hitung nilai r tabelnya. Bagaimana caranya ? Pada sel B3 tuliskan rumus berikut:  =TINV(B$2,$A3)/SQRT($A3+(TINV(B$2,$A3))^2).

Hasilnya sama kan ?. Tapi yang perlu diingat adalah, nilai r tabel ini adalah nilai dua arah. Kalau anda melakukan pengujian satu arah dengan α yang sama seperti diatas yaitu 5 %, maka Anda merubah alpha tersebut menjadi 10% (2 x 5 %).

sumber : junaidichaniago.wordpress.com/

Cara Praktis Menghitung r Tabel dengan SPSS

Pada SPSS kita juga bisa menghitung nilai r tabel.  Berbagai sumber menyebutkan bahwa untuk menghitung nilai r tabel kita harus terlebih dahulu menghitung nilai t  tabel . Hal ini karena nilai t tabel dihasilkan dari rumus sebagai berikut:

Dimana: r = nilai r tabel, t = nilai t tabel dan df = derajat bebas

Berdasarkan rumus tersebut, maka  pada SPSS dilakukan tahapan sebagai berikut: (kita ikuti cara panjang ini sebelum melihat cara ringkas agar bisa memahami prosesnya)

1. Buka program SPSS, kemudian buat variabel baru dengan nama misalnya nama variabelnya adalah df.

2. Kemudian isikan nilai derajat bebas (df) pada variabel tersebut. Terserah Sdr. mulai dari 1 sampai berapapun. Lihat contoh pada gambar berikut, misalnya dari df 1 – 5

3. Setelah itu klik Transform >  Compute Variable.  Akan muncul tampilan berikut: (hanya bagian yang penting yang ditampilkan)

Pada kotak isian Target Variable, isikan nama variabel untuk nilai t tabel yang akan kita hitung. Misalnya dalam contoh diatas kita beri nama t_0.05 (karena kita ingin menghitung t tabel dengan taraf signifikansi 5 %).

Pada kotak isian Numeric Expression: isikan rumus berikut:  IDF.T(0.95,df)

(Catatan: sebenarnya rumus tersebut bisa dibuat dengan menu dropdown, tapi tidak kita bahas disini).

Pada rumus diatas, angka pertama dalam kurung (sebelum tanda koma) yaitu 0.95 adalah tingkat/taraf keyakinan (level of confidence).  Taraf keyakinan ini  = 1 – α.  Nilai α (alpha) ini sendiri adalah tingkat/taraf signifikansi (level of significance). Jadi dalam contoh, misalnya kita ingin mencari nilai t tabel pada taraf signifikansi = 5 % (0.05), maka diisi pada rumus tersebut 1 – 0.05 = 0.95. (catatan: perhatikan perbedaannya dengan Excel. Pada rumus Excel, angka yang kita masukkan adalah langsung nilai α nya).

Selanjutnya, pada rumus diatas, setelah tanda koma adalah nama variabel tempat penyimpanan nilai derajat bebas yang telah kita tuliskan sebelumnya. Karena nama variabel yang kita buat sebelumnya adalah df, maka tulis df pada rumus tersebut.

4.  Setelah itu klik OK, maka akan muncul hasil sebagai berikut:

Kita sudah mendapatkan nilai t tabel. Sekarang lanjutkan pada tahap berikutnya dengan kembali meng klik Transform >  Compute Variable.  Akan muncul tampilan seperti pada tahapan 3. Tetapi sekarang pada kotak isian target variable kita tuliskan nama variabel untuk nilai r tabel yang akan kita hitung. Misalnya sebagai contoh kita beri nama r_0.05. Selanjutnya pada kotak isian Numeric Expression  isikan rumus berikut:  t_0.05/SQRT(df+t_0.05**2)

Setelah itu klik OK, maka akan muncul hasil sebagai berikut:

Nah, sudah kita dapatkan nilai r tabel disamping nilai t tabel.

Tapi, bagaimana kalau kita persingkat tahapannya dengan cara menggabungkan kedua rumus tersebut sehingga lebih praktis.

Mari kita ulangi tahapan ini dari awal, dengan penjelasan yang lebih ringkas

1. Buat variabel baru dengan nama variabel misalnya df. Isikan angka df misalnya dari 1-5
2. Klik Transform >  Compute Variable. Selanjutnya pada kotak isian Target Variable tuliskan nama variabel untuk nilai r tabel. Misalnya kita beri nama r_0.05, dan pada kotak isian Numeric Expression  isikan rumus berikut:  IDF.T(0.95,df)/SQRT(df+( IDF.T(0.95,df))**2)

Hasilnya sama kan ? Tapi yang perlu diingat adalah, nilai r tabel ini adalah nilai satu arah (catatan: berbeda dengan Metode Excel yang hasilnya adalah untuk dua arah). Kalau anda melakukan pengujian dua arah dengan α yang sama seperti diatas yaitu 5 %, maka Anda merubah alpha tersebut menjadi 2,5%  (5% / 2).

sumber: junaidichaniago.wordpress.com/

Cara Membaca Tabel F

Tulisan kali ini akan membahas mengenai cara membaca tabel F.

Salah satu bentuk struktur tabel F yang tersedia pada buku-buku statistik/ekonometrik  adalah sebagai berikut:

Judul tabel biasanya memuat keterangan mengenai nilai probabilita dari tabel F yang disajikan. Dalam contoh diatas, probabilitanya adalah 0,05.

Lalu apa itu yang dimaksud dengan probabilita pada tabel F tersebut ?

Dalam pengujian hipotesis, kita terlebih dahulu menetapkan tingkat/taraf signifikansi pengujian kita (biasanya disimbolkan dengan α (alpha)). Misalnya 1 %, 5 %, 10 % dan seterusnya. Nah, taraf/tingkat signifikansi tersebut yang merupakan probabilita dalam tabel ini.

Judul  masing-masing kolom mulai dari kolom kedua (angka yang dicetak tebal) dari tabel tersebut adalah derajat bebas/degree of freedom (df) untuk pembilang, atau dikenal dengan df1. Juga sering disimbolkan dalam tabel F dengan simbol N1 seperti tabel diatas.

Selanjutnya, judul masing-masing baris adalah derajat bebas/degree of freedom (df) untuk penyebut, atau dikenal dengan df2. Juga sering disimbolkan dalam tabel F dengan simbol N2 seperti tabel diatas.

Bagaimana menentukan  df1 (N1) dan df2 (N2) tersebut ?

Rumusnya:

df1 = k -1

df2 = n – k

dimana k adalah jumlah variabel (bebas + terikat) dan n adalah jumlah observasi/sampel pembentuk regresi.

Misalnya kita punya persamaan regresi dengan dua variabel bebas dan satu variabel terikat. Jumlah sampel pembentuk regresi tersebut sebanyak 10. Maka  df1= k-1 = 3 – 1 = 2 sedangkan df2 = n – k = 10 – 3 = 7

Jika pengujian dilakukan pada α = 5%, maka nilai F tabelnya adalah 4,74. Lihat pada N1=2 dan N2= 7 pada tabel diatas.

Sebagai catatan, juga terdapat format tampilan tabel F seperti gambar dibawah ini. Pada prinsipnya sama, yang membedakan adalah, probabilitanya di letakkan dalam satu kolom setelah N2.  Dengan demikian jika kita ingin mencari nilai F tabel misalnya  dengan df1=2, df2 = 2 dan α = 5%, maka lihat pada N1= 2, N2 =2 pada baris 0.05

Ok. Cukup sekian dulu. semoga bermanfaat . . .

sumber: junaidichaniago.wordpress.com/

Cara Membuat Tabel F dengan SPSS

Kali ini, kita akan membahas cara membuat tabel F dengan SPSS

Berikut tahapannya:

1. Buka program SPSS, kemudian buat variabel baru untuk pengisian derajat bebas. Variabel derajat bebas yang kita buat adalah untuk derajat bebas 2 (df2) atau penyebut. Misalnya kita beri nama variabel tersebut df_2.

2. Kemudian isikan nilai derajat bebas 2 (df2) pada variabel tersebut. Terserah Sdr. mulai dari 1 sampai berapapun. Lihat contoh pada gambar berikut, misalnya dari df 1 – 8

3. Setelah itu klik Transform >  Compute Variable.  Akan muncul tampilan berikut:

Pada kotak isian Target Variable, isikan nama variabel untuk nilai F tabel yang akan kita hitung. Misalnya dalam contoh diatas kita beri nama df1_1_0.05 (karena kita ingin menghitung F tabel dengan df1 (pembilang)=1 berapapun df2 nya, dan dengan α = 5 %)

Pada kotak isian Numeric Expression: isikan rumus berikut:  IDF.F(0.95,1,df_2)

(Catatan: sebenarnya rumus tersebut bisa dibuat dengan menu dropdown, tapi tidak kita bahas disini).

Pada rumus diatas, angka pertama dalam kurung (sebelum tanda koma) yaitu 0.95 adalah tingkat/taraf keyakinan (level of confidence).  Taraf keyakinan ini  = 1 – α.  Nilai  α  (alpha) ini sendiri adalah tingkat/taraf signifikansi (level of significance). Jadi dalam contoh, misalnya kita ingin mencari nilai t tabel pada taraf signifikansi = 5 % (0.05), maka diisi pada rumus tersebut 1 – 0.05 = 0.95. (catatan: perhatikan perbedaannya dengan Excel. Pada rumus Excel, angka yang kita masukkan adalah langsung nilai α nya).

Selanjutnya, pada rumus diatas, angka yang diapit tanda koma yaitu angka 1 adalah nilai df1 nya. Dan yang dibelakang tanda koma adalah nama variabel tempat penyimpanan nilai df2  yang telah kita tuliskan sebelumnya. Karena nama variabel yang kita buat sebelumnya adalah df_2, maka tulis df_2 pada rumus tersebut.

3. Setelah itu klik OK, maka akan muncul hasil sebagai berikut:

Kolom disamping df_2 adalah nilai F tabel untuk  df1=1 dan alpha = 0.05. Dengan cara yang sama, kita menghitung F tabel untuk nilai df1 lainnya (misalnya df1=2, df1=3  dstnya). Dengan cara yang sama kita juga mengganti α nya.

sumber:junaidichaniago.wordpress.com/

Tabel F lengkap Uji F

Tabel F yang digunakan untuk pengujian hipotesis (uji F)  biasanya telah tersedia dan dilampirkan pada buku-buku statistik atau ekonometrik. Namun demikian, tabel tersebut umumnya hanya tersedia secara berurut sampai derajat bebas (d.f./d.b) N2 = 30, kemudian meloncat ke d.f  = 40, d.f. = 60, d.f. 120 dan d.f. 200 . Tentunya, jika kita perhitungan kita memiliki derajat bebas N2 = 37 misalnya terpaksa harus melakukan interpolasi antara df = 30 dengan df 40.

Berikut ini saya lampirkan tabel F yang memuat nilai-nilai F mulai dari df (N2)  = 1 sampai df (N2) = 225 secara berurut. Silakan download disini.

Tabel F untuk Probabilita 0.01

Tabel F untuk Probabilita 0.05

Tabel F untuk Probabilita 0.10

Tabel F untuk Probabilita 0.25


sumber : http;//junaidichaniago.wordpress.com/

CARA ANALISIS BUTIR SOAL URAIAN/TUGAS DENGAN SPSS

SPSS merupakan sebuah program pengolah data yang sudah sangat dikenal di dalarn dunia pendidikan. Penggunaannya sangat mudah untuk dipahami. Semua data diketik di dalam format SPSS yang sudah disediakan. Setelah selesai, kemudian tinggal memilih statistik yang akan digunakan pada menu ANLYZE . Misalnya uji validitas butir atau reliabilitas tes, diklik pada menu ANLYZE kemudian pilih CORELATE, pilih BIVARIAT, untuk uji reliabilitas pilih RELIABILITY. Di samping itu, program ini dapat digunakan untuk analisis data kuantitatif secara umum.

Berikut ini disajikan Analisis Butir Soal Uraian/Praktik, sebagai salah satu contoh penggunaan program SPSS,  meliputi contoh pengetikan data dan langkah-langkah analisisnya. 

 

1. Siapkan data dalam Tabel

- Kolom menunjukkan jumlah butir   

- Baris menunjukkan jumlah siswa

Contoh data sebagai berikut

Siswa	S1	S2	S3	S4	S5	Jumlah
Aji Ari Amri Beni Budi Bambang Candra Citra Danuri Didik	6 5 5 4 4 4 3 3 2 1	7 7 6 5 4 4 3 3 2 2	7 8 6 6 7 5 4 3 3 3	8 7 8 7 6 6 5 5 4 3	7 7 7 6 6 5 4 3 2 2

 

2. Langkah-langkah analisis

- Klik "Variabel View"
- Ketik Siswa pada kolom "Name" kemudian klik pada kolom "Tipe" pilih/diklik "String"
- Ketik S1 pada kolom "Name" (di bawah Siswa) (S1= soal no 1)
- Ketik S2 pada kolom "Name" (di bawah S1)
- Ketik S3 dst. pada kolom "Name" (di bawah S2 dst)
- Ketik Jumlah pada kolom "Name"

Untuk menghitung "jumlah", klik "Transform Computer"

    Ketik "Jumlah" pada kotak "Target Variabel"
    Pada kotak "Numeric Expression" diisi/diketik S1 + S2 + S3 + S4 + S5
    Klik OK

Untuk menghitung validitas butir

• Klik Analyze

Correlate

Bivariate

• Kotak "Variables" diisi S1 S2 S3 S4 S5 Jumlah

• Klik Pearson, Klik Two-tailed, Klig Flag significant correlation.

• Klok OK.

Hasil analisis sebagai berikut.

Untuk menghitung Tingkat Kesukaran

• Klik Analyze

Descriptive Statistics

Frequencies

• Kotak Variables diisi S1 S2 S3 S4 S5
• Klik Statistics, Klik Mean
• Klik Continue
• Klik OK
  

Mean	Skormarks	TK
3.7 4.3 5.1 6.0 4.9	6 7 7 8 7

• Mean dan skor maksimal setiap butir dicatat, kemudian diketik dalam format SPSS
• Klik Transform

Compute

• Ketik TK pada kolom "Target Variable"
• Pada kotak "Numerik Expression"diisi/diketik Mean/Skormaks
• Klik OK.

Hasil analisis sebagai berikut.

Mean	Skormarks	TK
3.7 4.3 5.4 5.9 4.9	6 7 7 8 7	0.62 0.61 0.68 0.74 0.70

Untuk menghitung Reliabilitas Tes

• Analyze

          Scale

                    Reliability analyse

• Kotak "Items" diisi S1 S2 S3 S4 S5
• Klik Model: Pilih Alpha
• Klik Statistics: Pilih Item
• Klik "Continue"
• Klik OK.

Hasilnya adalah sebagai berikut

 

Kaidah Penetapan:
1) Jika  nilai Corrected Item - Total Correlation > dari angka r table, validitas terpenuhi.
2) Jika nilai Cronbach-Alpha > 0,8, reliabilitas butir terpenuhi.
3) Kriteria TK
0,00 – 0,30 = sukar
0,31 – 0,70 = sedang
0,71 – 1,00 = mudah

sumber: http://bunarti.net/

Cara Analisis Butir Soal Pilihan Ganda dan Uraian

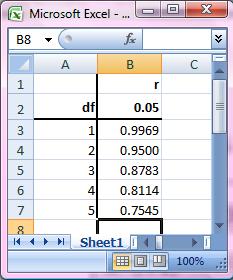
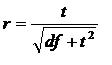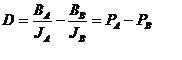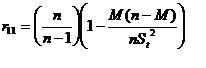Analisis soal dilakukan untuk mengetahui berfungsi tidaknya sebuah soal. Analisis pada umumnya dilakukan melalui dua cara, yaitu analisis kualitatif (qualitative control) dan analisis kuantitatif (quantitative control). Analisis kualitatif sering pula dinamakan sebagai validitas logis (logical validity) yang dilakukan sebelum soal digunakan. Gunanya untuk melihat berfungsi tidaknya sebuah soal. Analisis soal secara kuantitatif sering pula dinamakan sebagai validitas empiris (empirical validity) yang dilakukan untuk melihat lebih berfungsi tidaknya sebuah soal setelah soal itu diujicobakan kepada sampel yang representatif.

Salah satu tujuan dilakukannya analisis adalah untuk meningkatkan kualitas soal, yaitu apakah suatu soal (1) dapat diterima karena telah didukung oleh data statistic yang memadai, (2) diperbaiki, karena terbukti terdapat beberapa kelemahan, atau bahkan (3) tidak digunakan sama sekali karena terbukti secara empiris tidak berfungsi sama sekali.

Analisis Kualitatif. Yaitu berupa penelaahan yang dimaksudkan untuk menganalisis soal ditinjau dari segi teknis, isi, dan editorial. Analisis secara teknis dimaksudkan sebagai penelaahan soal berdasarkan prinsip-prinsip pengukuran dan format penulisan soal. Analisis secara isi dimaksudkan sebagai penelaahan khusus yang berkaitan dengan kelayakan pengetahuan yang ditanyakan. Analisis secara editorial dimaksudkan sebagai penelaahan yang khususnya berkaitan dengan keseluruhan format dan keajegan editorial dari soal yang satu ke soal yang lainnya.

Analisis kualitatif lainnya dapat juga dikategorikan dari segi materi, konstruksi, dan bahasa. Analisis materi dimaksudkan sebagai penelaahan yang berkaitan dengan substansi keilmuan yang ditanyakan dalam soal serta tingkat kemampuan yang sesuai dengan soal. Analisis konstruksi dimaksudkan sebagai penelaahan yang umumnya berkaitan dengan teknik penulisan soal. Analisis bahasa dimaksudkan sebagai penelaahan soal yang berkaitan dengan penggunaan bahasa Indonesia yang baik dan benar menurut EYD.

Analisis Kuantitatif. Digunakan untuk mengetahui sejauh mana soal dapat membedakan antara peserta tes yang kemampuannya tinggi dalam hal yang didefinisikan oleh kriteria dengan peserta tes yang kemampuannya rendah (melalui analisis statistik).

Analisis soal secara kuantitatif menekankan pada analisis karakteristik internal tes melalui data yang diperoleh secara empiris. Karakteristik internal secara kuantitatif dimaksudkan meliputi parameter soal tingkat kesukaran, daya pembeda, dan reliabilitas. Khusus soal-soal pilihan ganda, dua tambahan parameter yaitu dilihat dari peluang untuk menebak atau menjawab soal dengan benar dan berfungsi tidaknya pilihan jawaban, yaitu penyebaran semua alternatif jawaban dari subyek-subyek yang dites.

Tingkat Kesukaran. Ada beberapa alasan untuk menyatakan tingkat kesukaran soal. Bisa saja tingkat kesukaran soal ditentukan oleh kedalaman soal, kompleksitas, atau hal-hal lain yang berkaitan dengan kemampuan yang diukur oleh soal. Namun demikian, ketika kita mengkaji lebih mendalam terhadap tingkat kesukaran soal, akan sulit menentukan mengapa sebuah soal lebih sukar dibandingkan dengan soal yang lain.

Secara umum, menurut teori klasik, tingkat kesukaran dapat dinyatakan melalui beberapa cara diantaranya (1) proporsi menjawab benar, (2) skala kesukaran linear, (3) indeks Davis, dan (4) skala bivariat. Proporsi jawaban benar (p), yaitu jumlah peserta tes yang menjawab benar pada butir soal yang dianalisis dibandingkan dengan jumlah peserta tes seluruhnya merupakan tingkat kesukaran yang paling umum digunakan.

Intinya, bermutu atau tidaknya butir-butir item tes hasil belajar pertama-tama dapat diketahui dari derajat kesukaran atau taraf kesukaran yang dimiliki oleh masing-masing butir item tersebut. Butir-butir item tes hasil belajar dapat dinyatakan sebagai butir-butir item yang baik, apabila butir-butir item tersebut tidak terlalu sukar dan tidak pula terlalu mudah dengan kata lain derajat kesukaran item itu adalah sedang atau cukup. Angka yang dapat memberikan petunjuk mengenai tingkat kesulitan item itu dikenal dengan istilah difficulty index (angka indeks kesukaran item), yang dalam dunia evaluasi hasil belajar umumnya dilambangkan dengan huruf P, yaitu singkatan dari kata proportion (proporsi = proporsa).

Kategori Tingkat Kesukaran

Nilai p	Kategori
P < 0.3	Sukar
0.3 ≤ p ≤ 0.7	Sedang
P > 0.7	Mudah

Tindak Lanjut Hasil Analisis

Interpretasi Item	Tindak Lanjut
Sukar	1.        butir item dibuang atau didrop dan tidak dikeluarkan lagi dalam tes-tes hasil belajar yang akan datang  2.        diteliti ulang, dilacak, dan ditelusuri sehingga dapat diketahui faktor yang menyebabkan butir item yang bersangkutan sulit dijawab oleh testee, apakah kalimat soalnya kurang jelas, apakah petunjuk cara mengerjakan soalnya sulit dipahami, ataukah dalam soal tersebut terdapat istilah-istilah yang tidak jelas, dsb. Setelah dilakukan perbaikan, butir-butir item tersebut dikeluarkan lagi dalam tes hasil belajar yang akan datang. 3.        butir-butir yang terlalu sulit dapat digunakan kembali dalam tes (terutama tes seleksi) yang sifatnya sangat ketat.
Sedang	Butir item ini dapat dikeluarkan lagi dalam tes-tes hasil belajar pada waktu-waktu yang akan datang
Mudah	1.        butir item dibuang atau didrop dan tidak dikeluarkan lagi dalam tes-tes hasil belajar yang akan datang  2.        diteliti ulang, dilacak, dan ditelusuri sehingga dapat diketahui faktor yang menyebabkan butir item yang bersangkutan sulit dijawab oleh testee, apakah kalimat soalnya kurang jelas, apakah petunjuk cara mengerjakan solnya sulit dipahami, ataukah dalam soal tersebut terdapat istilah-istilah yang tidak jelas, dsb. Setelah dilakukan perbaikan, butir-butir item tersebut dikeluarkan lagi dalam tes hasil belajar yang akan datang. 3.        butir-butir yang terlalu sulit dapat digunakan kembali dalam tes (terutama tes seleksi) yang sifatnya longgar.

Daya Pembeda. Salah satu tujuan analisis kuantitatif soal adalah untuk menentukan dapat tidaknya suatu soal membedakan kelompok dalam aspek yang diukur sesuai dengan perbedaan yang ada dalam kelompok itu. Indeks yang digunakan dalam membedakan antara peserta tes yang berkemampuan rendah adalah indeks daya pembeda (item discrimination). Indeks daya pembeda soal-soal yang ditetapkan dari selisih proporsi yang menjawab dari masing-masing kelompok. Indeks ini menunjukkan kesesuaian antara fungsi soal dengan fungsi tes secara keseluruhan. Dengan demikian validitas soal ini sama dengan daya pembeda soal yaitu daya dalam membedakan antara peserta tes yang berkemampuan tinggi dengan peserta tes yang berkemampuan rendah.

Angka yang menunjukkan besarnya daya pembeda berkisar antara  -1 sampai dengan +1. Tanda negatif menunjukkan bahwa peserta tes yang kemampuannya rendah dapat menjawab benar sedangkan peserta tes yang kemampuannya tinggi menjawab salah. Dengan demikian soal indeks daya pembedanya negatif menunjukkan terbaliknya kualitas peserta.
Indeks diskriminasi item umumnya diberi lambang dengan huruf D (singkatan dari discriminatory power).

Indeks     Dsikriminasi Item (D)	Klasifikasi	Interpretasi
< 0,20	Poor	Butir item yang bersangkutan daya pembedanya lemah sekali (jelek), dianggap tidak memiliki daya pembeda yang baik
0,20 – 0,40	Satisfactory	Butir item yang bersangkutan telah memiliki daya pembeda yang cukup (sedang)
0,40 – 0,70	Good	Butir item yang bersangkutan telah memiliki daya pembeda yang baik
0,70 – 1,00	Excellent	Butir item yang bersangkutan  telah memiliki daya pembeda yang baik sekali
Bertanda negatif (-)	-	Butir item yang bersangkutan daya pembedanya negative sekali (jelek sekali)

Fungsi Distraktor. Pada saat membicarakan tes objektif bentuk multiple choice item tersebut untuk setiap butir item yang dikeluarkan dalam tes hasil belajar telah dilengkapi dengan beberapa kemungkinan jawab, atau yang sering dikenal dengan istilah option atau alternatif.

Option atau alternatif itu jumlahnya berkisar antara 3 sampai dengan 5 buah, dan dari kemungkinan-kemungkinan jawaban yang terpasang pada setiap butir item itu, salah satu diantaranya adalah merupakan jawaban betul (kunci jawaban), sedangkan sisanya adalah merupakan jawaban salah. Jawaban-jawaban salah itulah yang biasa dikenal dengan istilah distractor (pengecoh).

Menganalisis fungsi distraktor sering dikenal dengan istilah lain, yaitu : menganalisis pola penyebaran jawaban item. Adapun yang dimaksud dengan pola penyebaran jawaban item adalah suatu pola yang dapat menggambarkan bagaimana testee menentukan pilihan jawabnya terhadap kemungkinan-kemungkinan jawab yang telah dipasangkan pada setiap butir item.

Suatu kemungkinan dapat terjadi, yaitu bahwa dari keseluruhan alternatif yang dipasang pada butir item tertentu, sama sekali tidak dipilih oleh testee. Dengan kata lain, testee menyatakan “blangko”. Pernyataan blangko ini sering dikenal dengan istilah omiet dan biasa diberi lambang dengan huruf O.

Distraktor dinyatakan telah dapat menjalankan fungsinya dengan baik apabila distraktor tersebut sekurang-kurangnya sudah dipilih oleh 5 % dari seluruh peserta tes.

Sebagai tindak lanjut atas hasil penganalisaan terhadap fungsi distraktor tersebut maka distraktor yang sudah dapat menjalankan fungsinya dengan baik dapat dipakai lagi pada tes-tes yang akan datang, sedangkan distraktor yang belum dapat berfungsi dengan baik sebaiknya diperbaiki atau diganti dengan distraktor yang lain.

Reliabilitas. Keajegan dan ketidakajegan skor tes merupakan fokus  dari pengkajian tentang reliabilitas. Berikut adalah faktor yang mempengaruhi perolehan skor peserta didik (Thorndike) yang berakibat pada ketidakajegan terhadap skor.
Faktor yang Mempengaruhi Reliabilitas Skor

1	Karakteristik umum yang permanen peserta tes  a.       kemampuan yang dimiliki peserta didik dalam menghadapi tes b.      kemampuan umum dan teknik yang digunakan ketika mengambil tes c.       kemampuan umum untuk memahami petunjuk tes
2	Karakteristik khusus yang permanent peserta tes  a.       kemampuan peserta didik yang berkaitan dengan atribut yang diukur dalam sebuah tes b.      pengetahuan dan kemampuan khusus yang berkaitan dengan soal c.       keajegan respon peserta didik terhadap pilihan jawaban (misalnya mereka cenderung memberi jawaban A dari 4 alternatif yang disediakan atau cenderung memilih B dari soal benar salah yang disajikan) Khusus yang berkaitan dengan soal a.       pengetahuan khusus yang berkaitan dengan fakta atau konsep khusus b.      pengetahuan dan kemampuan khusus yang berkaitan dengan soal
3	Karakteristik umum yang temporer seperti :  a.       kesehatan b.      kelelahan c.       motivasi d.      gangguan emosi e.       kemampuan umum dan teknik yang digunakan ketika mengambil tes f.        pemahaman mekanisme tes g.       faktor panas, cahaya, ventilasi, dan lain sebagainya
4	Karakteristik khusus yang temporer seperti :  Khusus yang berkaitan dengan tes secara keseluruhan a.       pemahaman terhadap petunjuk tes b.      trik atau teknik-teknik mengatasi tes c.       pengalaman/latihan menghadapi tes terlebih lagi dalam tes psikomotor d.      kebiasaan menghadapi sebuah tes Khusus yang berkaitan dengan soal a.       fluktuasi ingatan yang dimiliki peserta didik b.      hal-hal yang berkaitan dengan perhatian dan keakuratan
5	Faktor penyelenggaraan  a.       waktu, bebas dari gangguan, dan petunjuk yang jelas b.      pengawasan c.       penskoran
6	Faktor yang tidak pernah diperhitungkan  a.       keberuntungan karena faktor menebak b.      mengingat soal yang telah dilihatnya

Untuk lebih jelasnya silahkan download :
contoh analisis soal pilihan ganda ( excel file )

Contoh analisis soal uraian  (  excel file ).

Contoh Analisi Butir Soal dan Analisis Ketuntasan Belajar dengan Excel

1. Analisis Pencapaian Ketuntasan Belajar dan Analisis Butir Soal (44-50 Siswa)Contoh: Format analisis ketuntasan belajar dan analisis butir soal berbasis program pengolah angka MS Excel untuk 44-50 siswa
   [download klik disini]
   —
2. Analisis Pencapaian Ketuntasan Belajar dan Analisis Butir Soal (37-43 Siswa)Contoh: Format analisis ketuntasan belajar dan analisis butir soal berbasis program pengolah angka MS Excel untuk 37-43 siswa [download klik disini]
   —
3. Analisis Pencapaian Ketuntasan Belajar dan Analisis Butir Soal (30-36 Siswa)Contoh : Format analisis ketuntasan belajar dan analisis butir soal berbasis program pengolah angka MS Excel untuk 30-36 siswa [download klik disini]
   —
4. Analisis Pencapaian Ketuntasan Belajar dan Analisis Butir Soal (23-29 Siswa)Contoh : Format analisis ketuntasan belajar dan analisis butir soal berbasis program pengolah angka MS Excel untuk 23-29 siswa [download klik disini]
   —
5. Analisis Ketuntasan Belajar dan Butir Soal untuk 250 SiswaContoh : Analisis ketuntasan belajar dan analisis butir soal untuk 250 siswa dengan jumlah soal 100 PG dan 10 Essay. Aplikasi ini berbasis aplikasi pengolah angka MS Office Excel [download klik disini]
   
6. Kisi-Kisi dan Materi Uji Olimpiade Sains BIDANG INFORMATIKA/KOMPUTER Disertai Contoh-contoh dan Pembahasan. [download klik disini]
   
   
   sumber: http://www.asrori.com/
   

Macam-macam Skala Pengukuran Statistik

Pengukuran dapat didefinisikan sebagai suatu proses sistimatik dalam menilai dan membedakan sesuatu obyek yang diukur. Pengukuran tersebut diatur menurut kaidah-kaidah tertentu. Kaidah-kaidah yang berbeda menghendaki skala serta pengukuran yang berbeda pula.

Dalam mengolah dan menganalisis data, kita sangat berkepentingan dengan sifat dasar skala pengukuran yang digunakan. Operasi-operasi matematik serta pilihan peralatan statistik yang digunakan dalam pengolahan data, pada dasarnya memiliki persyaratan tertentu dalam hal skala pengukuran datanya. Ketidaksesuaian antara skala pengukuran dengan operasi matematik /peralatan statistik yang digunakan akan menghasilkan kesimpulan yang bias dan tidak tepat/relevan.

Ada empat tipe pengukuran atau skala pengukuran yang digunakan dalam statistika, yakni: nominal, ordinal, interval, dan rasio.

1. Nominal

Skala Nominal merupakan skala yang paling lemah/rendah di antara skala pengukuran yang ada. Skala nominal hanya bisa membedakan benda atau peristiwa yang satu dengan yang lainnya berdasarkan nama (predikat). Skala pengukuran nominal digunakan untuk mengklasifikasi obyek, individual atau kelompok dalam bentuk kategori.

Pemberian angka atau simbol pada skala nomial tidak memiliki maksud kuantitatif hanya menunjukkan ada atau tidak adanya atribut atau karakteristik pada objek yang diukur. Misalnya, jenis kelamin diberi kode 1 untuk laki-laki dan kode 2 untuk perempuan. Angka ini hanya berfungsi sebagai label

kategori, tanpa memiliki nilai instrinsik dan tidak memiliki arti apa pun. Kita tidak bisa mengatakan perempuan dua kali dari laki-laki. Kita bisa saja mengkode laki-laki menjadi 2 dan perempuan dengan kode 1, atau bilangan apapun asal kodenya berbeda antara laki-laki dan perempuan. Misalnya lagi untuk agama, kita bisa mengkode 1=Islam, 2=Kristen, 3=Hindu, 4=Budha dstnya. Kita bisa menukar angka-angka tersebut, selama suatu karakteristik memiliki angka yang berbeda dengan karakteristik lainnya.

Karena tidak memiliki nilai instrinsik, maka angka-angka (kode-kode) yang kita berikan tersebut tidak memiliki sifat sebagaimana bilangan pada umumnya. Oleh karenanya, pada variabel dengan skala nominal tidak dapat diterapkan operasi matematika standar (aritmatik) seperti pengurangan, penjumlahan, perkalian, dan lainnya. Peralatan statistik yang sesuai dengan skala nominal adalah peralatan statistik yang berbasiskan (berdasarkan) jumlah dan proporsi seperti modus, distribusi frekuensi, Chi Square dan beberapa peralatan statistik non-parametrik lainnya.

2. Ordinal

Skala Ordinal ini lebih tinggi daripada skala nominal, dan sering juga disebut dengan skala peringkat. Hal ini karena dalam skala ordinal, lambang-lambang bilangan hasil pengukuran selain menunjukkan pembedaan juga menunjukkan urutan atau tingkatan obyek yang diukur menurut karakteristik tertentu.

Misalnya tingkat kepuasan seseorang terhadap produk. Bisa kita beri angka dengan 5=sangat puas, 4=puas, 3=kurang puas, 2=tidak puas dan 1=sangat tidak puas. Atau misalnya dalam suatu lomba, pemenangnya diberi peringkat 1,2,3 dstnya.

Dalam skala ordinal, tidak seperti skala nominal, ketika kita ingin mengganti angka-angkanya, harus dilakukan secara berurut dari besar ke kecil atau dari kecil ke besar. Jadi, tidak boleh kita buat 1=sangat puas, 2=tidak puas, 3=puas dstnya. Yang boleh adalah 1=sangat puas, 2=puas, 3=kurang puas dstnya.

Selain itu, yang perlu diperhatikan dari karakteristik skala ordinal adalah meskipun nilainya sudah memiliki batas yang jelas tetapi belum memiliki jarak (selisih). Kita tidak tahu berapa jarak kepuasan dari tidak puas ke kurang puas. Dengan kata lain juga, walaupun sangat puas kita beri angka 5 dan sangat tidak puas kita beri angka 1, kita tidak bisa mengatakan bahwa kepuasan yang sangat puas lima kali lebih tinggi dibandingkan yang sangat tidak puas.

Sebagaimana halnya pada skala nominal, pada skala ordinal kita juga tidak dapat menerapkan operasi matematika standar (aritmatik) seperti pengurangan, penjumlahan, perkalian, dan lainnya. Peralatan statistik yang sesuai dengan skala ordinal juga adalah peralatan statistik yang berbasiskan (berdasarkan) jumlah dan proporsi seperti modus, distribusi frekuensi, Chi Square dan beberapa peralatan statistik non-parametrik lainnya.

3. Interval

Skala interval mempunyai karakteristik seperti yang dimiliki oleh skala nominal dan ordinal dengan ditambah karakteristik lain, yaitu berupa adanya interval yang tetap. Dengan demikian, skala interval sudah memiliki nilai intrinsik, sudah memiliki jarak, tetapi jarak tersebut belum merupakan kelipatan. Pengertian “jarak belum merupakan kelipatan” ini kadang-kadang diartikan bahwa skala interval tidak memiliki nilai nol mutlak.

Misalnya pada pengukuran suhu. Kalau ada tiga daerah dengan suhu daerah A = 10^oC, daerah B = 15^oC dan daerah C=20^oC. Kita bisa mengatakan bahwa selisih suhu daerah B, 5^oC lebih panas dibandingkan daerah A, dan selisih suhu daerah C dengan daerah B adalah 5^oC. (Ini menunjukkan pengukuran interval sudah memiliki jarak yang tetap). Tetapi, kita tidak bisa mengatakan bahwa suhu daerah C dua kali lebih panas dibandingkan daerah A (artinya tidak bisa jadi kelipatan). Kenapa ? Karena dengan pengukuran yang lain, misalnya dengan Fahrenheit, di daerah A suhunya adalah 50^oF, di daerah B = 59^oF dan daerah C=68^oF. Artinya, dengan pengukuran Fahrenheit, daerah C tidak dua kali lebih panas dibandingkan daerah A, dan ini terjadi karena dalam derajat Fahrenheit titik nolnya pada 32, sedangkan dalam derajat Celcius titik nolnya pada 0.

Contoh lainnya, misalnya dua orang murid, si A mendapat nilai 70 sedangkan si B mendapat nilai 35. Kita tidak bisa mengatakan si A dua kali lebih pintar dibandingkan si B. (Kenapa ?)

Skala interval ini sudah benar-benar angka dan, kita sudah dapat menerapkan semua operasi matematika serta peralatan statistik kecuali yang berdasarkan pada rasio seperti koefisien variasi.

4. Skala rasio

Skala rasio adalah skala data dengan kualitas paling tinggi. Pada skala rasio, terdapat semua karakteristik skala nominal,ordinal dan skala interval ditambah dengan sifat adanya nilai nol yang bersifat mutlak. Nilai nol mutlak ini artinya adalah nilai dasar yang tidak bisa diubah meskipun menggunakan skala yang lain. Oleh karenanya, pada skala ratio, pengukuran sudah mempunyai nilai perbandingan/rasio.

Pengukuran-pengukuran dalam skala rasio yang sering digunakan adalah pengukuran tinggi dan berat. Misalnya berat benda A adalah 30 kg, sedangkan benda B adalah 60 kg. Maka dapat dikatakan bahwa benda B dua kali lebih berat dibandingkan benda A.

Sumber: http;//junaidichaniago.wordpress.com  

Cara Memasukkan Data pada SPSS (Step 4)

Postingan ini merupakan bagian terakhir dari seri tulisan mengenai cara input data pada SPSS. Untuk memahami bagian ini, silakan baca terlebih dahulu step 1 , step 2 dan step 3 sebelumnya.
Kali ini kita akan mempraktekkan pendefinisian variabel dengan data latihan yang telah diberikan pada tulisan sebelumnya.
Buka Program SPSS, kemudian masuk ke menu Variable View (dengan cara mengklik menu yang ada disudut kiri bawah)maka akan muncul tampilan berikut:

Pada baris pertama dari tampilan diatas, isikan Name dengan Responden. Pilih Type: String dengan cara klik sel dibawah Type, akan muncul titik tiga (…). Klik titik tiga tersebut akan muncul tampilan berikut:

Pilih (klik) String, isikan Characters=18 (ini adalah isian untuk Width) dan kemudian OK.
Selanjutnya isikan Label: Nama Responden. Isikan Column: 18. Pilih Align: Left (ketika anda klik sel dibawah Align akan muncul pilihan tersebut). Pilih Measure: Nominal (ketika anda klik sel dibawah Measure, akan muncul pilihan tersebut). Isian lainnya (Decimal, Values dan Missing), diabaikan karena untuk data tipe string tidak ada pilihan lain yang diberikan oleh program yaitu Decimal=0, Values=None dan Missing=None.
Selanjutnya pada baris kedua dari tampilan diatas, isikan Name: Sex. Pilih Type: Numeric dengan cara klik sel dibawah Type, akan muncul titik tiga (…). Klik titik tiga tersebut akan muncul tampilan berikut:

Pilih (klik) Numeric. Isikan Width=2. Isikan Decimal=0, kemudian OK.
Selanjutnya isikan Label: Jenis Kelamin Responden. Isikan Values dengan 1=laki-laki, 2= persempuan, dengan cara klik sel dibawah Values, akan muncul titik tiga (…). Klik titik tiga tersebut akan muncul tampilan berikut:

Isikan Value =1, Label = Laki-Laki, kemudian klik Add. Selanjutnya isikan Value = 2, Label = Perempuan kemudian klik Add. Setelah itu klik OK.
Biarkan default Missing dengan None. Isikan Column dengan 4. Pilih Align: Right dan pilih Measure: Nominal.
Selanjutnya pada baris ketiga dari tampilan diatas, isikan Name: Umur. Pilih Type: Numeric. Isikan Width: 3. Isikan Decimal: 0. Isikan Label dengan Umur Responden. Values=None. Missing=None. Isikan Column=5. Pilih Align: Right. Pilih Measure:Scale
Pada baris keempat dari tampilan diatas, isikan Name: Pendidikan. Pilih Type: Numeric. Isikan Width: 2. Isikan Decimal: 0. Isikan Label dengan Pendidikan Responden. Isikan Values dengan 1=SD, 2=SLTP, 3=SLTA, 4=D3, 5=S1. Missing=None. Isikan Column=8. Pilih Align: Right. Pilih Measure:Ordinal.
Pada baris kelima dari tampilan diatas, isikan Name:Pendapatan. Pilih Type: Numeric. Isikan Width: 4. Isikan Decimal: 0. Isikan Label dengan Pendapatan Responden. Values=None.
Pada variabel pendapatan dalam contoh kita, terdapat responden yang tidak memberikan informasi pendapatannya. Tentunya ini tidak bisa diinput dengan angka 0, karena akan mempengaruhi hasil perhitungan. Untuk itu, kita definisikan nilai missing dalam variabel ini (misalnya dengan angka 9999. Untuk mendefinisikan nilai missing ini, pilihlah angka yang tidak mungkin ada dalam data kita). Caranya adalah dengan klik sel dibawah Missing, akan muncul titik tiga (…). Klik titik tiga tersebut akan muncul tampilan berikut:

Klik Discret missing values, kemudian isikan angka 9999 pada kotak yang tersedia dibawahnya, kemudian klik OK.
Selanjutnya isikan Column=9. Pilih Align: Right. Pilih Measure:Scale.
Hasil dari tahapan-tahapan yang kita lakukan akan memberikan tampilan kira-kira sebagai berikut:

Setelah itu, klik menu Data View yang ada disudut kiri bawah, dan kita siap menginput data.
Berdasarkan data latihan kita sebelumnya, tampilan input data adalah sebagai berikut:

Selamat Mencoba . . .

Sumber: http;//junaidichaniago.wordpress.com  

Cara Memasukkan Data pada SPSS (Step 3)

Setelah memberikan dasar-dasar pendefinisian variabel untuk input data pada SPSS (lihat tulisan step 1 dan step 2), pada step 3 ini kita akan menggunakan data contoh untuk mempraktekkannya. Untuk memahami bagian ini, silakan baca dua bagian tulisan sebelumnya.

Sebagai latihan, misalnya kita akan menginput data hasil penelitian terdapat 18 responden penelitian sebagai berikut:

Pada contoh data latihan diatas, kita punya lima variabel (data) yang akan diinput yaitu nama responden, jenis kelamin, umur, pendidikan dan penghasilan. Mari kita definisikan masing-masing variabel sebagai berikut:

Variabel 1.
Nama Variabel: Responden
Type : String (karena variabel ini tidak berbentuk numerik)
Width: 18 (untuk data kita ini, jumlah karakter terbanyak 18)
Decimal : 0 (untuk data type string, desimal akan otomatis 0)
Label: Nama Responden
Values: None (untuk data type string, values akan otomatis none)
Missing: None (untuk data type string, missing akan otomatis none)
Column: 18 (ukuran kolom ini sesuaikan dengan jumlah karakter dari nama variabel atau maksimum karakter dari data pada variabel tersebut, mana yang paling banyak)
Align: Left (untuk data string sebaiknya dibuat rata kiri)
Measure: Nominal (untuk data string, pilih saja measure nominal)
Variabel 2.
Nama Variabel: Sex
Type : Numeric
Width: 2 (sebenarnya input data yang akan kita masukkan nanti hanya berupa kode 1 dan 2, atau hanya terdiri dari 1 karakter, tetapi width nya sebaiknya kita lebihkan 1 karakter)
Decimal : 0 (karena tidak memerlukan angka dibelakang koma)
Label: Jenis Kelamin Responden
Values: 1 = laki-laki, 2 = perempuan
Missing: None (karena informasi mengenai jenis kelamin tersedia pada semua responden)
Column: 4
Align: Rigth (untuk data numerik sebaiknya dibuat rata kanan)
Measure: Nominal (angka untuk pengkodean jenis kelamin ini, adalah termasuk data skala nominal)
Variabel 3.
Nama Variabel: Umur
Type : Numeric
Width: 3
Decimal : 0 (karena tidak memerlukan angka dibelakang koma)
Label: Umur Responden
Values: None (tidak ada pengkodean numerik untuk variabel ini)
Missing: None (karena informasi mengenai umur tersedia pada semua responden)
Column: 5
Align: Rigth (untuk data numerik sebaiknya dibuat rata kanan)
Measure: Scale (karena umur merupakan data berskala ratio)
Variabel 4.
Nama Variabel: Pendidikan
Type : Numeric
Width: 2 (karena pendidikan akan diinput dengan kode 1 – 5)
Decimal : 0 (karena tidak memerlukan angka dibelakang koma)
Label: Pendidikan Responden
Values: 1 = SD, 2= SLTP, 3= SLTA, 4= D3, 5= S1
Missing: None (karena informasi mengenai pendidikan tersedia pada semua responden)
Column: 8
Align: Rigth (untuk data numerik sebaiknya dibuat rata kanan)
Measure: Ordinal (karena pendidikan merupakan data berskala ordinal)
Variabel 5.
Nama Variabel: Pendapatan
Type : Numeric
Width: 4
Decimal : 0 (karena tidak memerlukan angka dibelakang koma)
Label: Pendapatan Responden (dalam ribuan Rp)
Values: None (tidak ada pengkodean numerik untuk variabel ini)
Missing: terdapat responden yang tidak memiliki informasi mengenai pendapatan. Untuk itu, sebagai latihan kita berikan kode 9999 untuk responden yang tidak kita dapatkan informasi pendapatannya tersebut
Column: 9
Align: Rigth (untuk data numerik sebaiknya dibuat rata kanan)
Measure: Scale(karena pendapatan merupakan data berskala ratio)

Selamat Mencoba . . .

Kunjungi juga "Cara Memasukkan Data pada SPSS (Step 4)"

Sumber: http;//junaidichaniago.wordpress.com 

Cara Memasukkan Data pada SPSS (Step 2)

Tulisan ini adalah sambungan dari Cara Memasukkan Data pada SPSS (Step 1).

Setelah menentukan nama variabel, jenis variabel, ukuran lebar dan desimal dari input data untuk masing-masing variabel, selanjutnya adalah mengisikan label untuk masing-masing variabel tersebut.
Label adalah semacam keterangan mengenai variabel. Berbeda dengan nama variabel yang terbatas hanya sampai 64 karakter, label dapat di buat sampai 256 karakter. Selain itu, label ini dapat menggunakan spasi maupun karakter-karakter yang tadinya tidak dapat digunakan pada nama variabel.
Berikutnya adalah menginputkan Values dari masing-masing variabel. Values ini secara khusus berguna jika data yang kita gunakan merupakan kode numerik (dalam bentuk angka) yang mewakili kategori non-numerik. (Misalnya kode 1 untuk laki-laki dan kode 2 untuk perempuan).
Untuk menginput values dari masing-masing variabel, klik sel di bawah Values, akan muncul titik tiga (…). Klik titik tiga tersebut, maka akan muncul tampilan berikut:

Isikan kode pada kotak Values dan labelnya pada kotak Label. Misalnya, kode 1 untuk Laki-laki. Setelah itu, klik Add. Lanjutkan untuk kode-kode berikutnya, setelah itu klik OK.
Setelah menentukan Values pada masing-masing variabel (jika ada), selanjutnya adalah menentukan nilai “missing” untuk masing-masing variabel. Menentukan nilai “missing” ini berguna, jika misalnya dalam pertanyaan survai, ada responden yang tidak memberikan/menolak memberikan jawaban, sehingga tidak tersedia data untuk diinput. Misalnya, jika ada responden yang menolak memberikan jawaban mengenai pendapatannya. Jika kita menginput jawaban responden tersebut dengan angka 0, maka dalam pengolahannya, SPSS akan memasukkan dalam perhitungan (sehingga akan berpengaruh terhadap rata-rata keseluruhan maupun terhadap distribusi frekuensi). Tetapi jika kita mendefinisikan suatu angka untuk menyatakan nilai missing tersebut, maka SPSS akan mengeluarkan dari perhitungan.
Untuk mendefinisikan nilai “missing” dari masing-masing variabel, klik sel di bawah “Missing”, akan muncul titik tiga (…). Klik titik tiga tersebut, maka akan muncul tampilan berikut:

Kita bisa mendefinisikan tiga deretan angka yang berbeda untuk nilai missing masing-masing variabel. Kita juga memberikan range nilai untuk mendefinisikan nilai missing tersebut. Dalam contoh tampilan diatas, misalnya kita mendefinisikan hanya satu deretan angka untuk nilai missing yaitu 99999. Dengan demikian, jika terdapat data yang kosong (atau tidak terisi) dari variabel kita, maka inputkan angka 99999. Setelah mendefinisikan nilai missing, klik OK.

Tahap selanjutnya adalah menentukan lebar kolom (Columns) dari worksheet SPSS untuk input data. Lebar kolom ini ditentukan minimal sama dengan “Width” variabel yang telah ditentukan sebelumnya.

Berikutnya adalah menentukan perataan (align) dari tampilan input data. Jika diklik sel dibawah align, akan muncul tiga pilihan yaitu left (rata kiri), right (rata kanan) dan center (rata tengah).
Selanjutnya, tahap terakhir dari pendefinisian variabel adalah menentukan skala pengukuran (measure) dari masing-masing variabel.
Ketika diklik sel dibawah Measure, akan terdapat tiga pilihan yairu Scale, Ordinal dan Nominal. Scale kita pilih jika skala pengukuran kita adalah skala interval atau ratio.
Setelah selesai dengan tahap terakhir pendefinisian variabel ini, klik kembali menu Data View (yang ada disudut kiri bawah).
Dengan cara ini, kita akan masuk ke worksheet SPSS dan siap untuk menginput data.

Selamat Mencoba . . .

Kunjungi juga "Cara Memasukkan Data pada SPSS (Step 3)"

Sumber: http;//junaidichaniago.wordpress.com

Cara Memasukkan Data pada SPSS (Step 1)

Pada posting ini, kita akan membahas cara menginput data dalam SPSS. Untuk menginput data tersebut, langkah-langkahnya sebagai berikut:
Buka Program SPSS. Pertama kali akan muncul tampilan sebagai berikut:

Tampilan tersebut adalah tampilan Data Editor dalam SPSS yang mempunyai fungsi utama untuk mendefinisikan, menginput, mengedit dan menampilkan data.
Di dalam SPSS, sebelum menginput data, definisikan terlebih dahulu data (variabel) yang akan diinput (meskipun ini bisa dilakukan belakangan, sebaiknya lakukan hal ini sebelum data diinput).
Perhatikan disudut kiri bawah dari tampilan data editor diatas. Disitu terdapat menu Data View (posisi kita saat ini, yang ditandai oleh tulisan yang lebih hitam) dan menu Variable View. Untuk mendefinisikan data (variabel), klik Variable View, maka akan muncul tampilan berikut:

Setiap baris dalam tampilan diatas digunakan untuk mendefinisikan satu variabel (data) yang akan diinput. Ada beberapa informasi yang perlu dimasukkan, yaitu:
Name: Isikan nama variabel. Persyaratan dalam pemberian nama variabel adalah:

1.) Nama variabel tidak boleh duplikasi dengan nama variabel lainnya.
2.) Nama variabel paling panjang hanya 64 karakter dan harus diawali oleh huruf atau @, #, $. Karakter berikutnya boleh kombinasi huruf, @, #, $ atau angka. Nama variabel yang diawali dengan tanda $ menunjukkan bahwa variabel tersebut adalah suatu variabel sistem. (Pembahasan mengenai variabel sistem akan dibahas pada tulisan-tulisan berikutnya. Untuk latihan kali ini, kita tidak akan menggunakan hal tersebut).
3.) Variabel tidak boleh mengandung spasi dan kata-kata kunci perintah SPSS yaitu ALL, AND, BY, EQ, GE, GT, LE, LT, NE, NOT, OR, TO, dan WITH.
Type: Definisikan tipe variabel. Ketika anda mengklik sel di bawah type, akan muncul titik tiga (…). Klik titik tiga tersebut, maka akan muncul tampilan berikut:

Dari tampilan diatas, terdapat beberapa pilihan tipe variabel sebagai berikut:

1.) Numeric. Variabel yang berbentuk angka
2.) Comma. Variabel numerik dengan tampilan koma untuk setiap 3 angka (memisahkan ribuan), dan titik untuk memisahkan desimal. Misalnya, jika data yang diinput adalah 2567932, maka akan ditampilkan dalam SPSS sebagai 2,567,932.00
3.) Dot. Variabel numerik dengan tampilan titik untuk setiap 3 angka (memisahkan ribuan), dan koma untuk memisahkan desimal. Misalnya, jika data yang diinput adalah 2567932, maka akan ditampilkan dalam SPSS sebagai 2.567.932,00
4.) Scientific notation. Variabel numerik dengan tampilan scientific. Misalnya, jika data yang diinput adalah 2567932, maka akan ditampilkan dalam SPSS sebagai 2.57E+006
5.) Date. Variabel numerik dengan nilai yang ditampilkan dalam format tanggal atau waktu. Jika anda pilih tipe data ini, akan muncul tampilan pilihan format tanggal atau waktu.
6.) Dollar. Variabel numerik dengan tampilan tanda $.
7.) Custom currency. Variabel numerik yang ditampilkan dalam format uang yang anda inginkan (custom currency) misalnya dalam bentuk Rp. Penggunaan pilihan format ini harus didefinisikan terlebih dahulu dalam menu Options pada Currency tab. (caranya akan kita bahas pada tulisan berikutnya)
8.) String. Variabel yang tidak berbentuk numerik (angka) dan karenanya tidak digunakan dalam perhitungan. Jenis ini juga dikenal sebagai variabel alphanumeric.

Setelah memilih jenis variabel,
Lanjutkan dengan mengisi Width, yaitu jumlah karakter (angka/huruf) maksimum dari data yang akan diinput.
Setelah itu, tentukan jumlah angka dibelakang koma yang (desimal) yang ingin ditampilkan. Selanjutnya klik OK. . . .

Selamat Mencoba . . .

Kunjungi juga "Cara Memasukkan Data pada SPSS (Step 2)"


Sumber: http;//junaidichaniago.wordpress.com

Cara Membaca Hasil Analisis Data dengan SPSS

Berikut ini adalah contoh cara membaca hasil analisis data dengan SPSS . . .

download

semoga bermanfaat . . .

CARA KOREKSI SOAL PILIHAN GANDA DENGAN EXCEL

Mau tau caranya......
Gini…intinya jawaban di tulis kembali di excel kemudian kunci jawaban juga ditulis, maka excel bisa mengoreksi dengan cepat dan mudah.
Jadi tidak perlu menulis ulang ketika nanti harus menyetor nilai ke wali kelas. Agar mudah input datanya jawaban siswa yang ABCDE diubah ke angka 12345. Artinya jika siswa menjawab A, maka diketik angka 1, jawaban B diketik angka 2 begitu seterusnya.


Njlimet….? Lho nggak! pasalnya begitu kita selesai membaca jawaban siswa(sambil input tentunya), maka nilai sudah langsung muncul.
Kenapa kudu diubah ke angka? GIni… kalau huruf ABCDE letak/posisinya pada papan ketik kan berjauhan, sementara kalau angka 12345 khan berdekatan. Agar lebih mudah lagi sel pada excel dibuat 5 jawaban-5 jawaban. Jadi setelah mengetik jawaban 1 s/d 5 tekan tombol TAB untuk membaca/menginputkan nomor 6 s/d 10.

Untuk lebih gamblangnya bisa diUNDUH disini contoh koreksi jawaban pilihan ganda dengan excel.
setelah di ketik setiap 5 soal, pada sel berikutnya adalah menggabungkan menjadi seluruh jawaban siswa menggunakan rumus =&. selanjutnya diadakan pemarkahan dengan membandingkan dengan kunci jawaban yang telah ditulis diatasnya.
JIka benar diberi skor 1 dan jika salah diberi skor 0(nol).
Rumusnya pakai fungsi logika = IF.
Sebenarnya pekerjaan ini telah dikerjakan sebelum menginputkan data, sehingga ketika input data praktis langsung melihat hasilnya

Keuntungan excel apa sih? Dengan koreksi dengan excel nantinya mudah untuk dilakukan analisis butir soal, sehingga bisa diketahui soal-soal mana yang sahih dan tidak.

sumber: http;//budies.wordpress.com/

CARA ANALISIS BUTIR SOAL DENGAN EXCEL

Pada postingan ini akan dibahas mengenai analisis butir soal menggunakan Excel. Dengan melakukan Analisis Butir Soal Pilihan Ganda Menggunakan Ms. Excel ini, akan diperoleh informasi sebagai berikut :
1. validitas suatu butir soal;
2. tingkat kesukaran suatu butir soal;
3. daya beda suatu butir soal;
4. reliabilitas soal.

Langkah-langkah yang ditempuh dalam analisis ini meliputi : pengumpulan data / lembar jawaban, koreksi, pemarkahan dan mengurutkan data serta menggolongkan data sesuai keperluan analisis. Jawaban yang benar diberi skor 1 dan jawaban salah diberi skor 0, selanjutnya siswa/data diurutkan berdasarkan perolehan skor. Siswa yang memperoleh Skor tertinggi ditempatkan pada urutan paling atas, skor terendah ditempatkan paling bawah.

1. Validitas Butir Soal
Soal yang valid harus dapat mengukur apa yang akan diukur. Untuk mengetahui Validitas butir soal digunakan rumus product momment, sebagai berikut:
keterangan:
r_xy = koefisien korelasi Pearson antara variabel X dan variabel Y
N = Jumlah responden
X = skor nilai tes tiap-tiap butir
Y = skor total
Untuk mengerjakan hal ini excel dapat mengerjakan dengan cepat dan mudah. Rumus yang digunakan adalah =PEARSON (data_hasil_ jawaban_siswa_pada_soal_no…, data_ jumlah_jawaban). Anda tidak perlu membuat tabel baru yang berisi kolom-kolom yang panjang dan banyak, cukup tabel hasil koreksi yang telah dibuat sebelumnya. Setelah didapat nilai (harga r_xy), selanjutnya nilai tersebut kita bandingkan dengan konstanta/tetapan korelasi. Tetapan korelasi tersebut dapat diperoleh dari buku-buku serial statistik, atau dapat membuat sendiri tabel korelasi momen produk dengan excel.(pada postingan sebelum ini…red) Untuk penelitian sosial atau penelitian pendidikan, taraf signifikan yang digunakan adalah taraf signifikan 5%. Sedangkan pada penelitian ilmiah yang memerlukan validitas tinggi seperti ketepatan obat terhadap suatu penyakit, kandungan unsur-unsur dalam suatu zat menggunakan taraf signifikan 1%. Pada analisis ini menggunakan taraf signifikan 5%, artinya kebenaran atau dalam hal ini validitasnya mencapai 95%. Jika r_xy  r_xy tabel maka soal tersebut tidak Valid dan jika r_{xy hitung}  r_xy tabel, maka soal tersebut valid.

2. Tingkat Kesukaran
Untuk menentukan tingkat kesukaran suatu tes (Suharsimi, 1986:198)dapat digunakan rumus:

keterangan :
P = indeks kesukaran
B = banyaknya siswa yang menjawab soal itu dengan benar,
JS = jumlah seluruh siswa peserta tes
Untuk mengiterpretasikan tingkat kesukaran butir tes digunakan kriteria sebagai berikut:
P antara 0,00 — 0,30 soal sukar;
P antara 0,30 — 0,70 soal sedang; dan
P antara 0,70 — 1,00 soal mudah.

3. Daya Beda Butir Soal
Untuk membedakan antara siswa yang pandai dengan siswa yang kurang pandai, siswa dikelompokkan menjadi tiga kelompok, yaitu kelompok atas 33%, kelompok bawah 33% dan sisanya adalah kelompok tengah. Rumus yang digunakan adalah :

keterangan:

D = daya pembeda

J_A = banyaknya peserta kelompok atas

J_B = banyaknya peserta kelompok bawah

B_A = banyaknya peserta kelompok atas yang menjawab benar

B_B = banyaknya peserta kelompok bawah yang menjawab benar

P_A = B_A / J_A = proporsi peserta kelompok atas yang menjawab benar

J_B = B_B / J_B = proporsi kelompok bawah yang menjawab benar

kriteria, jika D bernilai:

0,00–0,20 : soal jelek

0,20–0,40 : soal sedang/cukup

0,40–0,70 : soal baik

0,70–1,00 : soal baik sekali

4. Reliabilitas
Suatu tes dapat dikatakan mempunyai taraf kepercayaan yang tinggi jika tes dapat memberikan hasil yang tetap. Jadi pengertian reliabilitas tes berhubungan dengan masalah ketetapan(keajegan) hasil. Rumus yang digunakan untuk menentukan reliabilitas pada tes obyektif adalah K-R.21
keterangan:

r₁₁ = koefisien reliabilitas tes secara keseluruhan

n = banyaknya soal butir soal

M = Mean atau rerata skor soal yang valid

S = Simpangan baku

Untuk menginterpretasikan besarnya r₁₁

r₁₁ : 0,8–1,0 reliabilitas sangat tinggi

0,6–0,8 reliabilitas tinggi

0,4–0,6 reliabilitas cukup

0,2–0,4 reliabilitas rendah

0,0–0,2 reliabilitas sangat jelek

contoh hasil ulangan excel dapat diunduh di sini dan contoh pembuatan tabel produk momen dapat dilihat disini.

sumber: http;//budies.wordpress.com/